I’m working on Bayesian AB Tests for a showcase project.

Then I decided to do a quick memo on some principles regarding Bayesian AB Tests

Principles of Bayesian AB Tests

Steps:

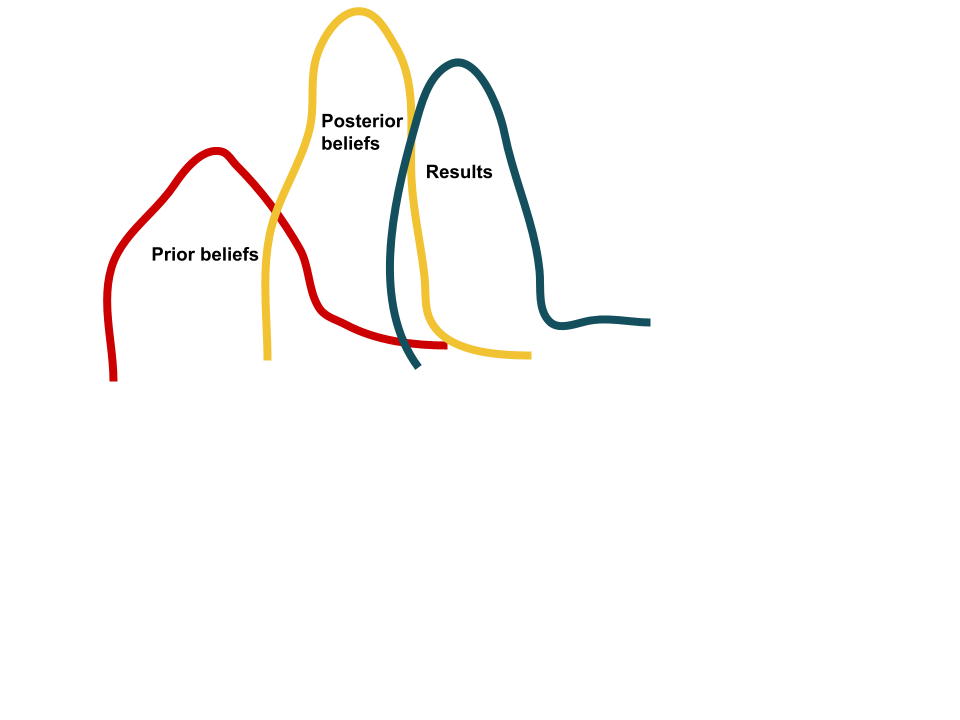
• You have beliefs (a priori).
• You do an experiment to test these beliefs.
• You get a result (a posteriori).
• You combine both to revise your first beliefs.

Example: you want to change the background colour of your website: from blue to green. You have 2 variants: blue (the old colour) and green (the new one) that you want to test.

You’ve done some research and know that in your industry, green is a colour generates 16% of conversion whereas blue generates 10% in your company.

These 16% and 10% are your prior beliefs. The experiment gives you some results. And the combination of both is the revision of your former beliefs: your posterior beliefs.

Set your prior beliefs as a beta distribution

To set a distribution as prior beliefs, you can use a Beta distribution.

The Beta distribution has two parameters: alpha => the number of successes beta => the number of failures

If you think that your new color will give 16% of conversion, you can set your beta distribution as: Beta(16, 84).

For a total of 100 trials, you get 16 successes and 86 failures.

Modulate your prior beliefs

The higher the numbers in a beta distribution, the more confident you are. High numbers will decrease the variance of your curve whereas low numbers flatten your curve.

• Beta(16, 84) if you’re confident enough
• Beta(8, 42) if you’re neutral
• Beta(4, 21) if you’re sceptical

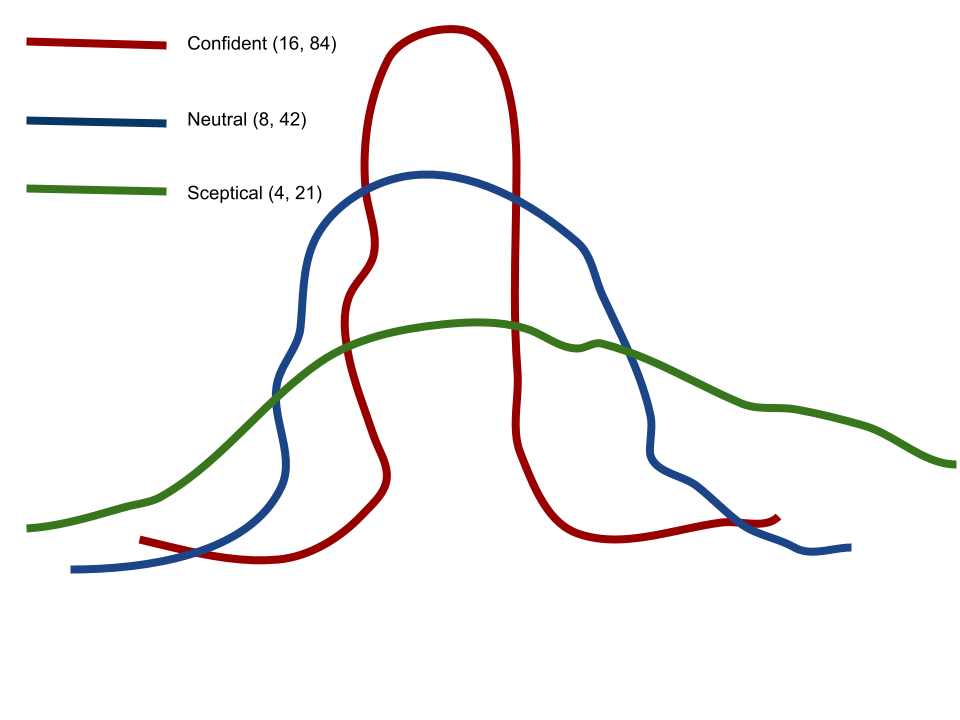
The ratio is the same (16%), but not the curve and then not the strength of your beliefs.